A Brief overview of Binomial and Poisson
Binomial Distribution:
Binomial Distributions are discrete probabilities used to represent the number of successful trials within a set number of independent tests. A Binomial distribution can be defined using two parameters; they include number of independent trials performed and their success probabilities per trial conducted independently. When there are only two outcomes per trial being used this distribution is employed so as to maintain constant success probabilities throughout them all.

Poisson Distribution:
Poisson distributions of probabilities represent the number of events over an interval in time. They are defined by one variable that either measures average rates of events occurring, or their average numbers; when random and independent events take place simultaneously they utilize this distribution model.
The Binomial Distribution is designed to identify successful trials within a set number of trials; while Poisson Distribution looks at events within an interval.
Importance of understanding the differences between Binomial and Poisson
Unerring both Binomial and Poisson Distributions is important for various reasons:
- Correct Modeling: Accurate representation and analysis require selecting an accurate distribution system, while any improper interpretation could lead to inaccurate conclusions and analysis. Choosing an ineffective distribution may produce subpar representation or analysis results in flawed conclusions and analyses.
- Calculating Probabilities Accurately: By understanding the differences between Binomial and Poisson distributions, you can more precisely calculate probabilities. Making informed choices regarding when to apply these distributions ensures your probability estimates reflect data characteristics for more precise results.
- Real-World Application: Both Binomial distribution and Poisson distribution have wide applications in numerous fields including finance, biology and manufacturing. Recognizing their distinction allows researchers, analysts and practitioners to analyze real world phenomena more precisely; such as estimating defects on an assembly line or anticipating how many customers might enter a shop.
- Data-Driven Decision Making: For informed data driven decision-making, understanding probability distributions is paramount to creating decisions with greater confidence and better results. Recognizing both Binomial and Poisson distributions allows decision makers to use them more confidently when selecting data driven solutions with confidence and improved outcomes.
- Statistical Inference: Differences between Binomial distribution and Poisson distribution have an enormous effect on statistical methods used for inference. Selecting the proper distribution can ensure proper application of hypotheses tests, confidence intervals and regression analyses; understanding these variations allows researchers to select appropriate statistical techniques and make valid inferences.
- Further Statistical Analysis: Understanding the difference between Binomial and Poisson Distributions forms the cornerstone of advanced statistical theory, opening doors for investigation of related distributions such as negative Binomial Distribution or geometric Distribution which build off their characteristics.
Understanding the differences between Binomial and Poisson Distributions is vital to accurate modeling, probabilistic calculations, data-driven decisions, statistical inference and further statistical analysis. Researchers and analysts who use such knowledge are better equipped to handle data more precisely and produce more reliable results from research projects and analyses.
Binomial
Binomial distributions are discrete probabilities used to measure the success of trials in multiple independent tests, commonly referred to as binomial tests. Their name comes from this concept involving multiple trials with only two potential outcomes success or failure.
Binomial Distributions are defined by two parameters – number of trials (n) and probability that any given trial succeeds (p). Each trial can only have two possible outcomes – success (often represented as “1”) or failure (typically represented as “0”.). This distribution assumes each attempt is independent with only two outcomes possible for every attempt – either success (usually represented as “1” in binomial format) or failure.
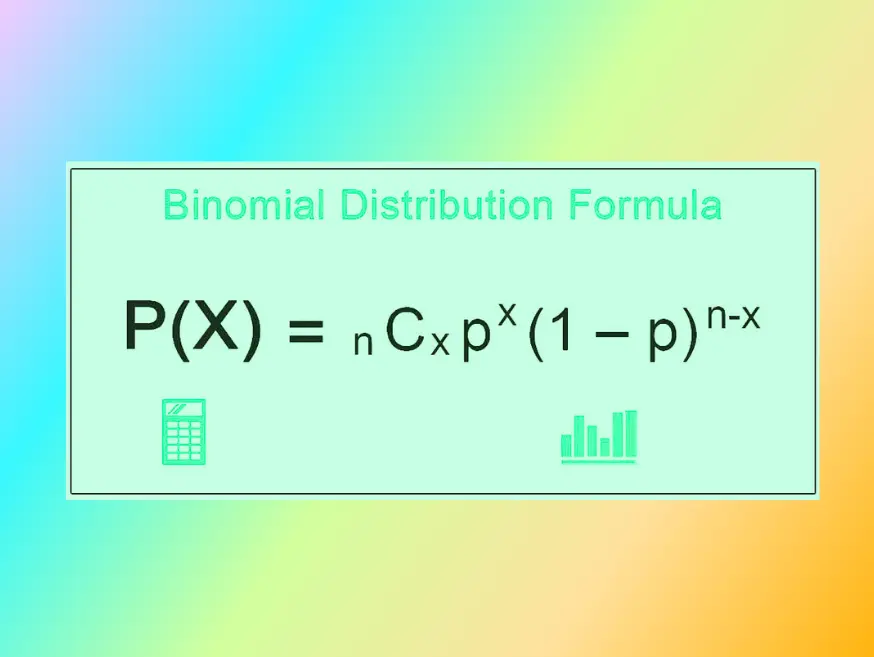
The probability mass function (PMF) of the Binomial distribution is given by:
P(X = k) = C(n, k) * p^k * (1 – p)^(n – k)
Where:
- P(X = K) measures the probability that exactly k successes will be observed from among n trials.
- C(n,k) represents all possible ways of selecting these trials successfully out of all available n trials with C(n,k) equaling 1. For this example we assume C(n -k) = 1.
- The probability that one out of k successes occurs can be represented as “pk.”
- To calculate failure probabilities use (1-p)(n-k).
The Binomial distribution is commonly used in various applications, including:
- Modeling the likelihood of successful outcomes across an independent set of experiments. For instance, tracking how often heads appear when flipping coins.
- Also measuring how many defective products exist within samples taken from production lines.
- Estimating the probability that certain events will take place over an exact set of trials is one way of doing statistical modeling.
Some key characteristics of the Binomial distribution include:
- Mean (expected value), or mean m, of any distribution can be calculated with this equation.
- M=n*p and variance can be computed with this expression: S2 = (n-p-1).
- When p is equal to zero or below 0.5 it forms an ideal distribution; once above this value the distribution becomes increasingly unbalanced.
Binomial Distribution provides an effective tool for analyzing and forecasting the number of successful trials across an set number of independent tests when each has only two possible outcomes.
Poisson
Poisson distribution is a discrete probability model used to simulate how often events happen within any period. The term was first coined by French mathematician Simeon-Denis Poisson in 1954.
Poisson distributions can be described using one parameter (typically denoted l, or lambda), representing the average rate of events within any specified interval. Assumptions about independence and randomness make this distribution ideal: it remains constant across its span of study.
The probability mass function (PMF) of the Poisson distribution is given by:
P(X = k) = (e^(-λ) * λ^k) / k!
Where:
- P(X = K) measures the probability that exactly k events will take place during an interval.
- Its base logarithm is approximately 2.71828
- The average rate or average number occurring per interval during said interval is given as L.
- K is simply its number of occurrences.
Poisson distribution can be utilized in numerous fields to estimate the probability of an event taking place over a specific time or area. It is frequently employed in situations like:
- Modelling call centre calls in an hour.
- Estimating accidents on specific road segments every day.
- And measuring customer entry into shops over an extended time span are among many of the many other issues addressed by APECS.
The Poisson distribution has several notable characteristics:
- When both variance and mean (average)
- The distribution are equal, it has an uneven bias to the right.
- As average rates increase, its shape becomes more even and approaches normal distribution.
Poisson distribution can be used to investigate and predict rare events within an interval, where events occur independently and at random.
Differences between Binomial and Poisson
Binomial distribution and Poisson distribution are discrete probabilities used to measure success when counting or succeeding at something. They differ significantly in terms of assumptions and applications. Here are some key differences between them:
1. Nature of Events:
- Binomial Distributions: Binomial distributions can be used when there are an equal number of independent trials that could either lead to success or failure; regardless of how each one turns out. Each result does not influence future ones.
- Poisson Distribution: Poisson distribution applies when events happen independently and randomly over a specific time interval or area, without an influence from previous outcomes affecting probabilities for subsequent ones. It allows multiple possible outcomes without altering probabilities for subsequent ones.
2. Parameters:
- Binomial Distributions: Binomial distributions can be defined using two parameters; number of trials conducted and probability that each will succeed (p).
- Poisson Distribution: A Poisson distribution can be defined by one parameter known as lambda that describes its average rate or number of events over any interval period. This value represents either rate of events occurring per unit time interval, or numbers occurring per interval period.
3. Assumptions:
- Binomial Distribution: Binomial distribution assumes each trial is independent with an equal and constant success probability, and keeps rate constant over the entire interval.
- Poisson Distribution: Poisson distribution assumes events occur randomly with rates remaining constant over the entire interval.
4. Applications:
- Binomial Distribution: This distribution can be used to model scenarios involving fixed number trials with two possible outcomes; such as simulating coin flips or defective items found within an sample population.
- Poisson Distribution: This distribution can help estimate how many events occur during a specified time interval, such as phone calls per hour, accidents on certain road segments daily, or customers entering shops during specified periods.
5. Shape of Distribution:
- Binomial Distribution: With increasing numbers, its distribution tends to become symmetric.
- Poisson Distribution: As L increases, this distribution becomes increasingly normalized and symmetric.
Realize the distinctions among these distributions is critical to applying them accurately in real-life scenarios, statistical analyses and other applications.
Choosing between Binomial and Poisson
Your specific requirements and characteristics for solving any given problem will ultimately dictate which distribution strategy should be employed, so be mindful when choosing one. Take these aspects into consideration before selecting any particular distribution model.
Nature of the Data:
- Binomial Distribution: Binomial is the appropriate distribution when the data involves multiple independent trials with two possible outcomes – like flipping a coin multiple times to count how many heads it lands on.
- Poisson Distribution: When modeling random and independent events that happen frequently over time or space, such as accidents on certain roads each day, Poisson distribution can be used. A prime example would be modeling their number.
Parameters and Assumptions:
- Binomial Distribution: To estimate its probability, the Binomial distribute requires two parameters; number of trials n and probability that each will succeed (p). Each trial assumes it has an independent chance for success and should therefore not interfere with each other in terms of probability.
- Poisson Distribution: With this distribution model, there is one parameter, Lambda (l), representing either the average rate or number of events or their average frequency; it relies on randomness being at play when events happen while remaining constant over time.
Sample Size and Probability of Success:
- Binomial Distributions: Binomial distributions can be effective when sample size (number of trials or n) and probability of success (p), are both small but not excessively so.
- Prison Distribution: Poisson distribution is appropriate when sample size (n), average rate of error per trial or L, is relatively large or moderate in magnitude.
Shape of Distribution:
- Binomial Distribution: With increasing numbers, its distribution becomes more balanced.
- Poisson Distribution: Skewed right, this distribution peaks near average rate but as L increases it becomes symmetrical like normal distributions would typically do.
Real-World Context and Interpretation:
Take into consideration both the context and interpretation of your results before drawing any definitive conclusions from them. Binomial distributions may be appropriate when trying to estimate the probability that a certain number of successful trials will happen within a specific number of trials. Poisson distribution may better suit you when trying to estimate how likely an event or series of events is occurring within an interval period.
Selecting between Binomial or Poisson distributions depends upon the specific characteristics and assumptions aligned with a problem as well as desired interpretation of said data. In order to conduct accurate and appropriate analyses, it’s vitally important to thoroughly assess all these factors and their potential influence.
Conclusion
Binomial and Poisson distributions are essential tools for understanding and analyzing probability in various fields. While the Binomial distribution focuses on the number of successes in a fixed number of trials, the Poisson distribution deals with the occurrences of events in a fixed interval. Their unique characteristics and applications make them indispensable in data science, decision-making, and statistical



