Scalar and Vector Quantity have both magnitude and direction as components. Understanding their differences is vitally important across numerous scientific disciplines, especially advanced concepts and calculations. In this article we’ll look into their applications, properties and importance within science.
Definition of Scalar Quantity
A scalar quantity is a type of physical quantity that is described solely by its magnitude or size and does not have any associated direction. Scalar quantities are quantities that can be completely specified by a single real number or value. Scalar quantities are characterized by their magnitude or numerical value, which represents the amount or intensity of the quantity being measured.
Scalar quantities are independent of the coordinate system and do not involve any directional information. They are usually expressed using appropriate units of measurement. Scalar quantities encompass time, temperature and mass as well as speed and energy.
Mathematical properties and rules pertaining to real numbers are utilized when performing operations on scalar amounts such as multiplication, division, addition or subtraction. Concatenating two scalar amounts always results in another one of them – it always yields something back into another scalar sum.
It’s important to note that scalar quantities do not convey information about the direction or orientation of physical phenomena. To describe quantities that involve both magnitude and direction, we need to use vector quantities.
Definition of Vector Quantity
Vector quantities can be defined both by their size or magnitude and direction in space, respectively. A vector’s magnitude and direction can be graphically represented with an arrow. Its length represents both aspects.
Vector quantities can be seen as possessing both numerical (magnitude) and spatial orientation properties; examples of vector quantities would include force, momentum and electric fields.
Vector algebra is used when performing operations on vector quantities such as addition, subtraction and multiplication. When performing addition, both magnitudes and directions must be considered. When subtracting vectors using their negation as subtractor. Scalar multiplication involves multiplying one vector magnitude with another real number (scalar); however its direction remains unaltered during multiplication.
Vectors can often be described by using either angles or coordinate systems as indicators for direction, different vectors may require various coordinate systems depending on their context.
Vector quantities represent quantities with both magnitude and direction, providing for more accurate descriptions of phenomena in both physics and engineering.
Importance of understanding the difference between Scalar and Vector Quantity
Understanding the difference between Scalar Quantities and Vector Quantities is of utmost importance in various scientific disciplines and real-world applications.
Here are some reasons this distinction:
- Mathematical Operations: Mathematical operations for vectors and scalars differ drastically; standard arithmetic applies when adding, subtracting or multiplying with vectors while multiplication of standard arithmetic applies when dealing with them. Understanding these mathematical operations is vital when solving problems and performing accurate calculations in both physics and engineering fields.
- Physical Phenomena: Scalar and vector quantities represent different aspects of physical phenomena. Scalar quantities, such as temperature or mass, provide information about the magnitude or intensity of a quantity, but they do not convey any direction. Vector quantities, such as velocity or force, capture both magnitude and direction, which are crucial for understanding motion, forces, and interactions in the physical world.
- Coordinate Systems: Vector quantities are often described using coordinate systems, such as Cartesian or polar coordinates, which provide a framework for specifying both magnitude and direction. Understanding how to express vector quantities in different coordinate systems and how to manipulate them is essential for accurate measurements, calculations, and analysis in various fields.
- Problem Solving: Many real-world problems involve both scalar and vector quantities. By distinguishing between the two, one can appropriately analyze and solve problems involving physical quantities. As part of any problem-solving strategy, it’s crucial that one can differentiate between scalar quantities and vector quantities when formulating solutions and applying problem solving techniques.
- Communication and Representation: Differentiating between scalar and vector quantities aids effective communication and representation of physical phenomena. When describing a phenomenon or presenting data, understanding whether a quantity is scalar or vector enables clear and concise communication of the relevant information. Graphical representations, such as diagrams or charts, can be appropriately constructed to visually depict vector quantities with their direction and magnitudes.
Understanding the distinction between scalar and vector quantities is vital for accurate mathematical calculations, comprehensive understanding of physical phenomena, problem-solving, effective communication, and proper representation of data. Mastery of these concepts is essential for success in various scientific disciplines and practical applications.
What is Scalar Quantity?

Scalar quantities are physical quantities that are described solely by their magnitude or numerical value and do not possess any associated direction. These quantities can be completely specified by a single real number or value. Scalar quantities are characterized by their magnitude, which represents the size, amount, or intensity of the quantity being measured.
Here are some examples of scalar quantities:
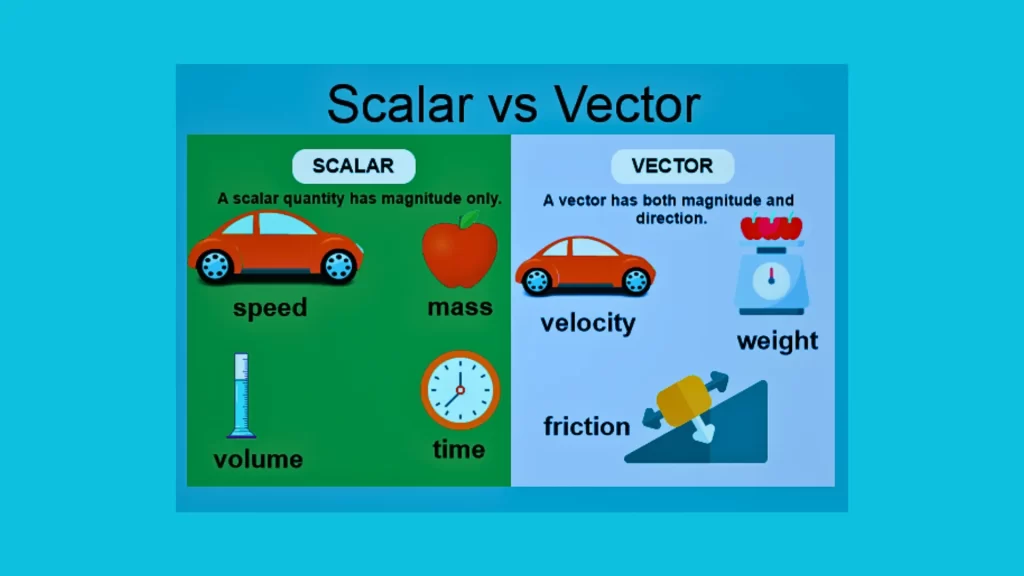
- Time: Time is a scalar quantity that represents the duration or interval between events. Measured units include seconds, minutes or hours.
- Temperature: Temperature is an enumerated number which measures heat or cold in relation to body or environment, usually expressed as either degrees Celsius (degC), or Kelvins (K).
- Mass: Mass is a scalar quantity that represents the amount of matter in an object. It quantifies the inertia or resistance to changes in motion. Mass is commonly measured in units like kilograms (kg) or pounds (lb).
- Speed: Speed is a scalar quantity that measures the rate of change of distance over time. It represents how fast an object is moving without considering its direction. Speed can be measured either in meters per second or miles per hour.
- Energy: Energy measures an object or system’s ability to perform work. Energy can take various forms such as thermal, kinetic and potential energy; its units of measurement include joules (J) or calories (cal).
- Volume: Volume is an empirical measurement used to describe how much space an object or substance occupies in relation to itself, typically expressed in either cubic meters or liters.
Scalar quantities can be added, subtracted, multiplied, and divided using standard arithmetic operations, as they follow the rules and properties of real numbers. The result of combining scalar quantities is always another scalar quantity.
What is Vector Quantity?
Vector quantities are physical quantities that have both magnitude and direction. Unlike scalar quantities, vector quantities require the specification of both magnitude and direction to fully describe them. Vectors can be represented graphically using arrows. Their length represents magnitude while direction represents their orientation in space.
Here are some examples of vector quantities:
- Displacement: Displacement (disp) is the measurement of change in an object’s location over time; indicated by an arrow from initial to final positions.
- Velocity: Velocity is a vector quantity that combines the magnitude of speed with a specific direction of motion. It represents the rate of change of displacement over time. Velocity of an object is defined by both its speed and direction of travel.
- Acceleration: Acceleration is the measure of velocity change. More specifically, acceleration indicates how quickly velocity fluctuates over time.
- Force: Force is a vector quantity that describes the interaction between objects and causes changes in their motion. It has both magnitude and direction and is represented by an arrow pointing in the direction of the force applied.
- Momentum: Momentum is the vector quantity which describes an object’s movement over time and space; its measurement depends on both mass and speed of its motion. It has both magnitude and direction and is important in understanding collisions and interactions between objects.
- Electric Field: In physics, the electric field is a vector quantity that describes the effect of electric charges on other charges in the surrounding space. It has both magnitude and direction, indicating the direction in which a positive charge would move if placed in the field.
Vector quantities are manipulated using vector algebra, which involves vector addition, subtraction, and scalar multiplication. The rules for adding and subtracting vectors consider both magnitude and direction, resulting in a resultant vector. Scalar multiplication of a vector involves multiplying the magnitude of the vector by a scalar (real number), while keeping the direction unchanged.
Understanding vector quantities is essential in various fields, including physics, engineering, and navigation, as they provide a more complete description of physical phenomena that involve both magnitude and direction.
Differences Between Scalar and Vector Quantity
There are several key differences between scalar quantities and vector quantities. Understanding these distinctions is crucial for accurately describing and analyzing various physical phenomena.
Here are the main differences between scalar and vector quantities:
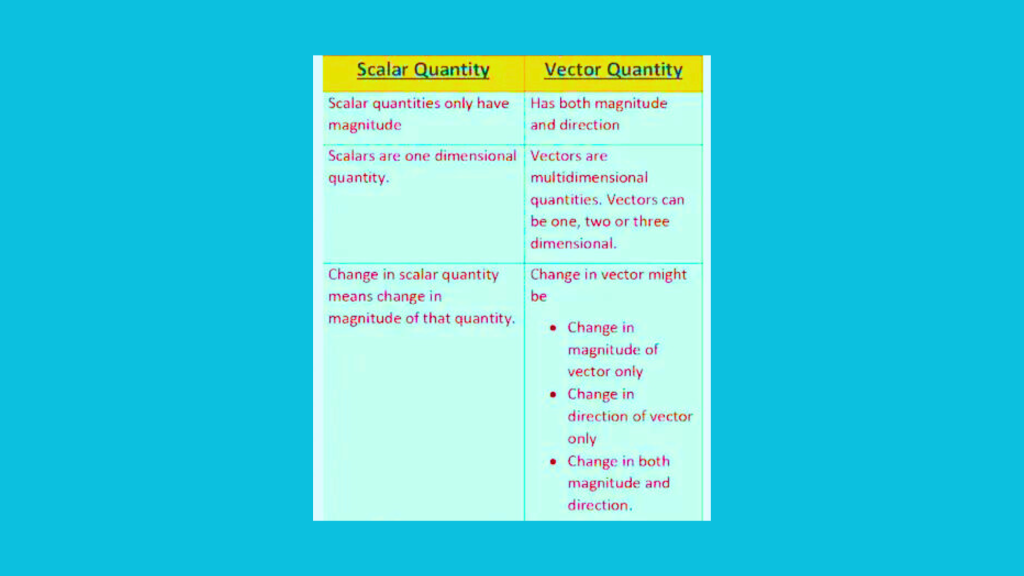
- Magnitude and Direction:
- Scalar Quantity: Scalar quantities are described solely by their magnitude or numerical value. They represent the size, amount, or intensity of a physical quantity. Scalars have no associated direction.
- Vector Quantity: Vector quantities have both magnitude and direction. In addition to representing the size or intensity, vectors also indicate the orientation or spatial direction of the quantity.
- Mathematical Representation and Operations:
- Scalar Quantity: Scalar quantities can be represented by a single real number or value. They follow the rules of arithmetic and can be added, subtracted, multiplied, and divided using standard mathematical operations.
- Vector Quantity: Vector quantities are represented by arrows or directed line segments. The length of the arrow represents the magnitude, while the arrow’s direction indicates the vector’s direction. Vector addition, subtraction, and scalar multiplication involve considering both the magnitudes and directions of the vectors.
- Physical Significance:
- Scalar Quantity: Scalar quantities are often associated with quantities that do not possess directionality in their physical nature. They represent properties such as time, temperature, mass, speed, and energy.
- Vector Quantity: Vector quantities are used to describe physical phenomena that involve both magnitude and direction. They are associated with quantities like displacement, velocity, acceleration, force, and momentum, which require directionality to fully characterize the phenomena.
- Representation and Notation:
- Scalar Quantity: Scalars are typically represented using italicized letters (e.g., t for time, T for temperature) or in mathematical equations as variables.
- Vector Quantity: Vectors are often denoted by boldface letters (e.g., 𝐝 for displacement, 𝐯 for velocity) or with arrows placed above the letters (e.g., →d for displacement, →v for velocity).
- Graphical Representation:
- Scalar Quantity: Scalar quantities are usually represented by a single point or value on a graph, without any directional information.
- Vector Quantity: Vector quantities are represented graphically by arrows or directed line segments, where the arrow’s length represents the magnitude, and its direction represents the vector’s direction.
Understanding the differences between scalar quantities and vector quantities is essential for accurately representing and analyzing physical phenomena, performing calculations, and solving problems in various scientific and engineering fields.
Similarities of Scalar and Vector Quantity
While Scalar and Vector quantities have distinct characteristics, there are a few similarities between them:
- Measurement Units: Both scalar and vector quantities are associated with specific measurement units. Whether it is time, temperature, displacement, or velocity, scalar and vector quantities are quantified using units such as seconds, degrees Celsius, meters, or kilometers per hour. The units enable consistent measurement and comparison of these quantities.
- Mathematical Operations: Scalar and vector quantities both undergo mathematical operations, albeit with different rules. Scalars can be added, subtracted, multiplied, and divided using standard arithmetic operations. Vectors undergo vector addition, subtraction, and scalar multiplication, which involve considering both magnitude and direction.
- Representation in Equations: Scalar and vector quantities can be represented using symbols in mathematical equations. Scalars are typically denoted by italicized letters (e.g., t for time, T for temperature), while vectors are represented by boldface letters (e.g., 𝐝 for displacement, 𝐯 for velocity). Equations involving both scalar and vector quantities can be combined to describe complex physical phenomena.
- Combination in Physical Laws: Scalar and vector quantities can coexist within physical laws and principles. For instance, Newton’s second law of motion, F = ma, combines a scalar quantity (mass, m) with a vector quantity (acceleration, a) to describe the relationship between force (a vector) and the motion of an object.
While these similarities exist, it is important to note that the fundamental distinction between scalar and vector quantities lies in their respective characteristics of magnitude and direction. Scalars are solely described by magnitude, while vectors require both magnitude and direction to fully represent physical phenomena.
Applications of Scalar and Vector Quantity
Scalar and vector quantities have diverse applications across various scientific disciplines and real-world scenarios.
Here are some examples of how scalar and vector quantities are applied:
Applications of Scalar Quantities:
- Timekeeping: Scalar quantities like time are fundamental for measuring and keeping track of events, scheduling activities, and coordinating processes in fields such as astronomy, physics, and everyday life.
- Temperature Control: Scalar quantities such as temperature are crucial for controlling and regulating environments, maintaining comfort levels, and ensuring optimal functioning of systems like heating, ventilation, and air conditioning (HVAC) systems.
- Mass Calculation: Scalar quantities like mass are essential for determining the amount of material present in objects, calculating dosages in pharmaceuticals, analyzing chemical reactions, and measuring the load-bearing capacity of structures.
- Energy Consumption: Scalar quantities like energy are used to quantify and manage energy consumption in industries, residential buildings, and transportation systems. They play a vital role in energy efficiency evaluations and cost calculations.
- Fluid Dynamics: Scalar quantities such as pressure and density are extensively employed in fluid mechanics for studying fluid behavior, designing hydraulic systems, analyzing flow rates, and optimizing processes in fields like aerospace, civil engineering, and environmental science.
Applications of Vector Quantities:
- Motion Analysis: Vector quantities like displacement, velocity, and acceleration are employed in analyzing and describing the motion of objects. They are crucial in fields such as physics, engineering, and sports biomechanics for studying trajectories, evaluating performance, and designing motion control systems.
- Forces and Mechanics: Vector quantities like force and momentum are fundamental in mechanics for understanding the effects of external influences on objects’ motion, calculating the net force acting on systems, and analyzing collisions.
- Navigation and Geolocation: Vector quantities are extensively used in navigation systems, GPS technology, and mapping applications. They help determine positions, plan routes, and calculate distances and directions between locations.
- Electromagnetism: Vector quantities such as electric and magnetic fields are essential in electrical engineering, telecommunications, and electronics. They are used for analyzing electromagnetic wave propagation, designing antennas, and calculating signal strengths.
- Vector Visualization: Vector quantities find applications in data visualization and computer graphics. They are utilized for representing flow patterns, visualizing vector fields, and simulating natural phenomena like fluid flows, weather patterns, and simulations in virtual environments.
These are just a few examples showcasing the broad applications of scalar and vector quantities. The understanding and appropriate utilization of these concepts are crucial in a wide range of scientific, engineering, and technological fields.
Conclusion
Scalars and Vectors are essential mathematical entities that provide us with a deeper understanding of the physical world. While scalars represent quantities with magnitude alone, vectors encompass both magnitude and direction, making them invaluable tools in various scientific, engineering, and mathematical disciplines.



